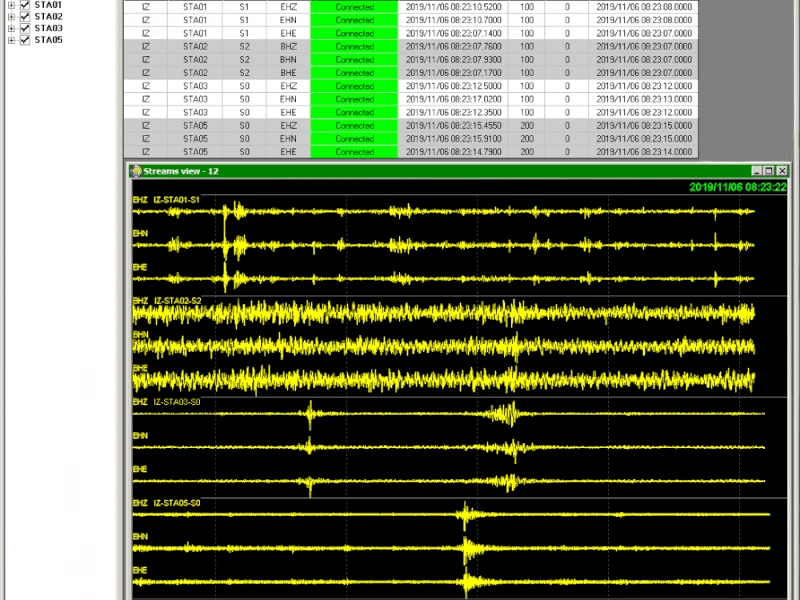
Detecting Noise Harassment with Smart Airborne Acoustic Monitoring

Noise harassment—whether from persistent loud neighbors, industrial operations, or environmental disturbances—can have serious impacts on health and well-being. Chronic exposure to unwanted sound is linked to stress, anxiety, insomnia, and reduced concentration.

While traditional noise complaints rely on subjective reporting, advances in airborne acoustic monitoring now provide a precise, verifiable way to identify and document noise harassment events.

What Is Airborne Acoustic Monitoring?

Airborne acoustic monitoring is the process of capturing and analyzing sound waves traveling through air using highly sensitive microphones and sensors. Unlike simple sound level meters, these systems:

  • Continuously record noise levels in real time.
  • Detect specific patterns and frequencies associated with harassment or nuisance sounds.
  • Store and analyze historical data, creating a digital record for verification.

This makes the technology particularly useful for communities, workplaces, and legal authorities dealing with ongoing noise disputes.

Why Use Acoustic Monitoring for Noise Harassment?

1. Objective Evidence
Instead of relying solely on personal accounts, acoustic monitoring provides time-stamped, quantifiable data on noise events.

2. Continuous Surveillance
Systems can run 24/7, ensuring no event goes undocumented, even at night when disturbances are most disruptive.

3. Pattern Recognition
Advanced software can differentiate between normal background noise and intentional harassment, including:

  • Repetitive banging or thumping
  • High-frequency tones designed to irritate
  • Amplified music or speech targeted at neighbors

Introducing the QuakeLogic AIR Infrasound Monitor

For clients seeking a professional-grade solution, QuakeLogic proudly offers the AIR Infrasound Monitor. This advanced system is purpose-built for detecting and analyzing both audible noise and infrasound (below human hearing range), making it uniquely powerful for identifying subtle or intentionally disruptive harassment sources.

Key Advantages of AIR

  • High-precision infrasound detection to capture low-frequency signals often missed by conventional microphones.

Whether for residents facing noise harassment, municipalities enforcing regulations, or industries monitoring compliance, AIR provides verifiable data.

Why QuakeLogic?

At QuakeLogic, we specialize in advanced monitoring solutions for seismic, vibration, and acoustic. Our AIR Infrasound Monitor represents the cutting edge of noise harassment detection—bridging the gap between traditional sound level meters and intelligent, cloud-connected monitoring systems.

Conclusion

Noise harassment is more than an inconvenience—it’s a public health issue. With the right tools, individuals, communities, and organizations can detect, document, and resolve noise disputes effectively. QuakeLogic’s AIR Infrasound Monitor transforms subjective complaints into actionable evidence, empowering a healthier, quieter future.

Learn more about the AIR Infrasound Monitor here

👉 Take control of your environment today. Explore the AIR Infrasound Monitor and empower your community with the evidence needed to ensure a healthier, quieter future.

ASCE 7-22 VS30 Site Classification Requirements: DoReMi® MASW Turnkey Seismograph + SEISMOWIN Solution

Streamline ASCE 7-22 VS30 Site Classification Using DoReMi® MASW Seismographs with SEISMOWIN

The latest ASCE 7-22 standard requires Vs30 shear wave velocity measurements as a key parameter for site classification and seismic design. This shift makes reliable, efficient, and accurate seismic characterization of soils more critical than ever for geotechnical engineers, structural designers, and regulatory compliance.

The DoReMi® Seismograph is the perfect solution. Its digital telemetry system with embedded electronics offers unmatched efficiency, scalability, and modularity. Each channel operates as an independent seismograph, enabling networks from 1 to 255 channels for projects of any scale. Lightweight, durable, and powered by a rechargeable battery with smart standby mode, DoReMi® ensures seamless field deployment and uninterrupted operation. With over 15 years of proven reliability and hundreds of global clients, it is a trusted standard in seismic surveys and geotechnical site investigations.

Paired with SEISMOWIN, a complete seismic data management and analysis suite, the DoReMi® becomes a turnkey solution for Vs30 determination. SEISMOWIN’s MASW (Multichannel Analysis of Surface Waves) and ReMi (Refraction Microtremor) modules provide advanced tools to analyze both active-source surface waves and ambient noise, ensuring flexibility in diverse field conditions. MASW delivers detailed S-wave velocity profiles comparable to borehole logs—without being affected by velocity reversals—while ReMi excels in noisy environments where passive surveys are preferable.

Together, DoReMi® + SEISMOWIN empower engineers to quickly and confidently obtain Vs30 values required under ASCE 7-22, streamlining the entire workflow from data acquisition to final reporting. In-house design, production, and support guarantee fast service, expert training, and customization to meet project-specific needs.

✅ Turnkey Package Includes:

  • DoReMi® Seismograph with 12 or 24+ channels and 4.5 Hz geophones
  • SEISMOWIN software with MASW & ReMi modules
  • Complete field-ready system with battery, cabling, and accessories
  • Training and technical support

With this integrated solution, compliance with ASCE 7-22 site classification requirements is no longer a challenge—it’s an opportunity to deliver faster, more reliable, and cost-effective results.

DoReMi Seismograph: The All-in-One Solution

Key Features of DoReMi Seismograph:

  • Modular Design: Scalable to support 1 to 255 channels, allowing flexible configurations for diverse projects.
  • Embedded Recording Electronics: Electronics are embedded in the cable, reducing electromagnetic interference.
  • Lightweight & Portable: Easily transported with a cable wheeler, ensuring smooth deployment in remote sites.
  • Integrated Battery System: Built-in rechargeable battery ensures continuous and independent operation.
  • Noise Reduction: Digitalization near the geophone minimizes noise and prevents data loss or crosstalk.
  • Flexible Sensor Integration: Supports 4.5 Hz geophones, downhole sensors (SS-BH-5C), and other seismic equipment.
  • Free Analysis Software: Compatible with any processing software, simplifying data management and interpretation.

Advanced Software for Seamless Operation

The DoReMi Seismograph is complemented by advanced software tools, designed to streamline on-site data quality checks and post-processing workflows.

Key Software Capabilities:

  • Pre-Shot Noise Monitoring: Ensures data integrity before acquisition.
  • Downhole & Surface Data Management: Simplifies different acquisition scenarios.
  • Signal Inversion & Overlapping: For SH shots and advanced processing.
  • Data Filtering & Spectral Analysis: Advanced tools for FK and FV analysis.
  • Roll-Along Acquisition: Simplifies large-area surveys.
  • HVSR Preview: Horizontal-to-Vertical Spectral Ratio preview for subsurface mapping.
  • Multi-Language Support: Available in English, Italian, and Chinese.

Applications of DoReMi Seismograph

  • Seismic Hazard Assessment: Earthquake resilience site characterization.
  • Geophysical Exploration: MASW, ReMi, Refraction, Reflection, and Downhole surveys.
  • Infrastructure Projects: Foundation analysis and underground mapping.
  • Resource Exploration: Aquifer detection, oil and gas reservoir profiling.
  • Urban Development: Roadbed evaluations and soil stiffness assessments.

Data Outputs from DoReMi Seismograph

  1. 1D Shear Wave Velocity Profile:
    • Vertical shear-wave velocity analysis for site characterization.
  2. 2D Shear Wave Velocity Profile:
    • Comprehensive subsurface mapping when multiple acquisitions are performed.

These outputs are essential for geotechnical engineers, seismologists, and urban planners in making informed decisions.

Why Choose DoReMi Seismograph for MASW and ReMi Surveys?

  • Dual Capability: Seamlessly supports both MASW and ReMi techniques.
  • High Precision: Noise-free, reliable data acquisition.
  • Scalable Design: Flexible configurations from 1 to 255 channels.
  • Advanced Software Integration: Simplified analysis and data management.
  • Portability: Lightweight design with modular architecture.
  • Expert Support: Dedicated training, support, and consultation from QuakeLogic.
👉 Order Your DOREMI Equipment

Conclusion

The DoReMi Seismograph by QuakeLogic represents a state-of-the-art solution for MASW and ReMi seismic surveys, offering unmatched flexibility, precision, and reliability. Whether it’s mapping shallow shear-wave velocity using MASW or profiling deeper subsurface layers with ReMi, DoReMi delivers results you can trust.

Experience precision, reliability, and innovation with the DoReMi Seismograph—your trusted partner in seismic exploration.

📞 For more information or to request a demo, contact us at:
Phone: +1-916-899-0391
Email: sales@quakelogic.net
Website: https://products.quakelogic.net/product/doremi-seismographs/

QUAKEMATE: Bringing Earthquake Science to Classrooms

Affordable Shake Table for K-12 & Universities

At QuakeLogic, we believe that hands-on learning is the most powerful way to inspire the next generation of scientists and engineers. That’s why we developed QUAKEMATE, a small-scale, classroom-ready shake table designed to make earthquake science engaging, practical, and affordable.

Why QUAKEMATE?

Earthquakes are powerful reminders of nature’s force, and understanding them is vital for building safer communities. QUAKEMATE gives students the opportunity to experience realistic seismic simulations right inside their classroom or lab — no advanced equipment or technical setup required.

With QUAKEMATE, students can:

  • Test Model Structures: Build and shake bridges, towers, and houses to see how they react.
  • Learn Resonant Frequencies: Discover why some structures collapse while others survive.
  • Explore Engineering Concepts: Apply physics and design principles to strengthen their models.
  • Engage in Teamwork: Collaborate on exciting experiments that bring theory to life.

Key Features

  • Realistic Simulation – Replicates seismic wave patterns to mimic earthquake behavior.
  • Advanced LED Control – Adjustable cycles (0–30 Hz) to match real-world P-wave frequencies.
  • Custom Sequences – Program up to 8 minutes of unique shaking patterns.
  • Classroom-Friendly Design – Lightweight, quiet, and safe for students of all ages.
  • Durable Build – Built for long-term educational use at an accessible price.
  • Hands-On STEM Learning – Includes plywood plates, bolts, and washers for simulating loads.

Specifications at a Glance

  • Power: 110V & 220V compatible
  • Payload: Up to 30 kg
  • Operation: Standalone (no computer needed)
  • Control: LED display, programmable sequences
  • Extras: Comes with setup guide and student project ideas

A Powerful Educational Tool

QUAKEMATE isn’t just a lab device — it’s an educational experience. From elementary schools to engineering programs, this shake table helps students connect theory with practice, making lessons in physics, geology, engineering, and resilience come alive.

Imagine a classroom where students build miniature skyscrapers, program a quake sequence, and then watch how their designs perform under simulated seismic stress. With QUAKEMATE, seeing is believing.

Frequently Asked Questions

Q: Is QUAKEMATE safe for classrooms?
Yes — it’s designed for safe, risk-free use in K-12 and university environments.

Q: What kind of structures can be tested?
From popsicle-stick bridges to LEGO® towers, any small-scale model can be tested.

Q: Does it replicate real earthquakes?
It mimics seismic motion patterns, helping students understand how structures respond.

Q: Can students program their own shake patterns?
Absolutely — up to 8 minutes of custom shaking can be set.

Who Is QUAKEMATE For?

  • K-12 Schools – Hands-on STEM learning for science fairs, labs, and afterschool programs.
  • Universities – Introductory tool for civil engineering, physics, and seismology courses.
  • STEM Outreach Programs – Demonstrations for public education and disaster preparedness.

Conclusion

The QUAKEMATE Shake Table is an affordable, portable, and powerful tool for making earthquake education exciting and interactive. It bridges the gap between classroom theory and real-world science, empowering students to become future engineers, innovators, and problem-solvers.

👉 Ready to bring QUAKEMATE to your classroom or lab?
📞 Call us at +1-916-899-0391 | 📧 Email: sales@quakelogic.net
🌐 Visit us at https://products.quakelogic.net/product/eqs-tremor-table/